Dans cet article nous allons voir comment nos souvenirs en Mathématiques peuvent nous aider à résoudre un problème pratique.
Nous allons utiliser le théorème d’Al-Kashi (qui généralise le théorème de Pythagore) afin de calculer la valeur d’un l’angle dans un triangle quelconque que nous allons créer à l’écran à partir de trois points A,B et C.
1 – Le Problème informatique
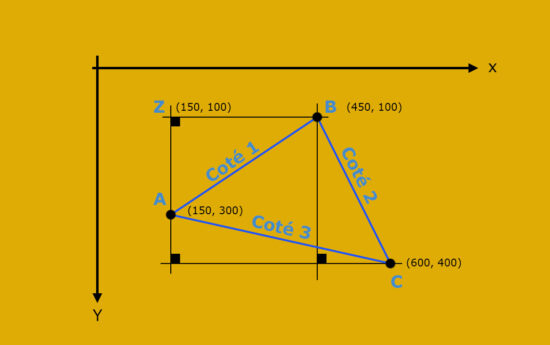
Lorsque nous interagissons avec un ordinateur, le moyen le plus simple de créer un triangle est de désigner ses trois points (A, B et C) avec la souris ou le stylet de la tablette graphique.
Il est possible ensuite de récupérer les coordonnées cartésiennes de ces trois points mais cela est insuffisant pour calculer la mesure d’un angle de ce triangle: nous avons besoin de déterminer la longueur de ses trois cotés (coté1, coté2 et coté 3).
Nous devrons donc calculer ces trois cotés pour ensuite être en mesure d’appliquer le théorème d’Al-Kashi.
2 – Le théorème d’Al-Kashi
Vous connaissez déjà probablement le théorème de Pythagore que nous dit que:
Théorème de Pythagore:
Si un triangle est rectangle, le carré de la longueur de l’hypoténuse (ou côté opposé à l’angle droit) est égal à la somme des carrés des longueurs des deux autres côtés.
Ce théorème de Pythagore ne nous permettra pas de résoudre notre problème mais il va nous être utile dans notre cheminement.
Il existe une autre formule, le théorème d’Al-Kashi, qui va nous permettre de résoudre le problème.
Le théorème d’Al-Kashi, ou théorème de Pythagore généralisé, ou encore loi des cosinus est un théorème mathématique qui est utilisé en géométrie pour connaître la longueur d’un côté, ou un angle, d’un triangle quelconque, à partir de la longueur des autres côtés et de la mesure de l’angle opposé.
Théorème d’Al-Kashi:
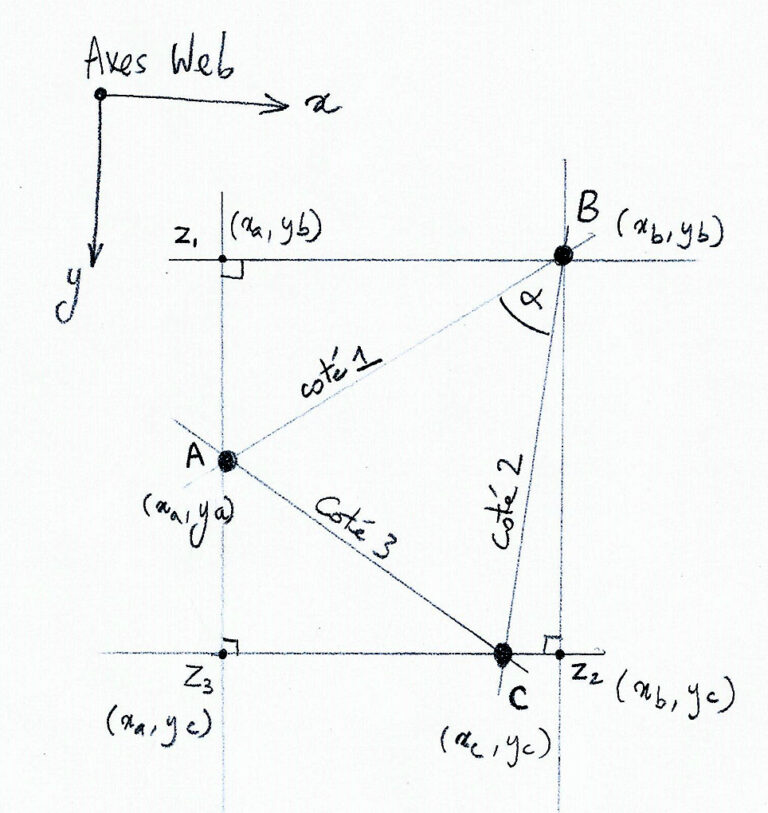
On définit le triangle ABC (avec coté1 = AB, coté2 = BC et coté3 = AC)
pour calculer un angle alpha quelconque du triangle ABC on considère les cotés adjacents à l’angle (ici coté1 et coté2) et le coté opposé (ici coté3, qui serait l’hypoténuse si alpha = 90°)
la formule définit que le cosinus de l’angle recherché est égal à la somme des carrés de coté1 et coté2 moins le carré de coté3, le tout divisé par le double du produit de coté1 et coté2.
Il suffit ensuite d’appliquer le cosinus inverse (arccos) au résultat obtenu pour obtenir la valeur de l’angle (en radians)
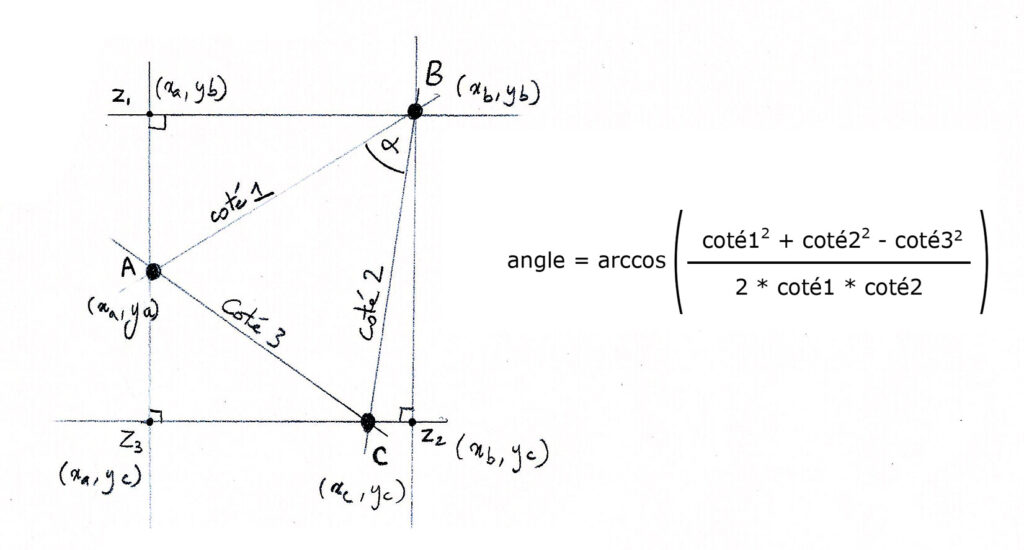
Pourquoi ce théorème est-il la généralisation du théorème de Pythagore?
Si le triangle est un triangle rectangle et si considérons alpha comme étant l’ange droit, qui vaut 90°, le coté3 devient l’hypoténuse et nous retrouvons l’égalité selon laquelle la somme des carrés des cotés (coté1² + coté2²) est égale au carré de l’hypoténuse (coté3²), conformément à la formule de Pythagore.
Avec notre formule d’Al-Kashi, l’expression (coté1² + coté2² – coté3²) devient ainsi égale à 0, et comme nous savons aussi que le cosinus d’un angle de 90° est égal à 0, nous vérifions bien que le théorème de Pythagore s’applique dans ce cas.
La formule devient angle = arccos (0)
3 – La solution Informatique
La théorie, c’est bien beau … et certes nécessaire … mais maintenant nous devons dessiner les droites (les cotés du triangle) et ensuite calculer les angles, sur notre écran, avec la souris.
3.1 – Le constat
Sur un ordinateur, avec Javascript, nous pouvons récupérer les coordonnées cartésiennes d’un point sur lequel nous avons cliqué. Dans ce contexte, l’origine du repère cartésien est en haut et à gauche de l’écran, l’axe des ordonnées Y étant dirigé vers le bas

Ces données, seules, ne nous permettent pas de calculer un angle du triangle formé par les trois points.
3.2 – L’étape intermédiaire nécessaire
Pour calculer la longueur de chaque coté du triangle nous devons extrapoler un triangle rectangle sur chaque couple de points du triangle (3 fois). Les coordonnées du point local Z seront données par la projection verticale de A et la projection horizontale de B, dans le cas du triangle AZB.
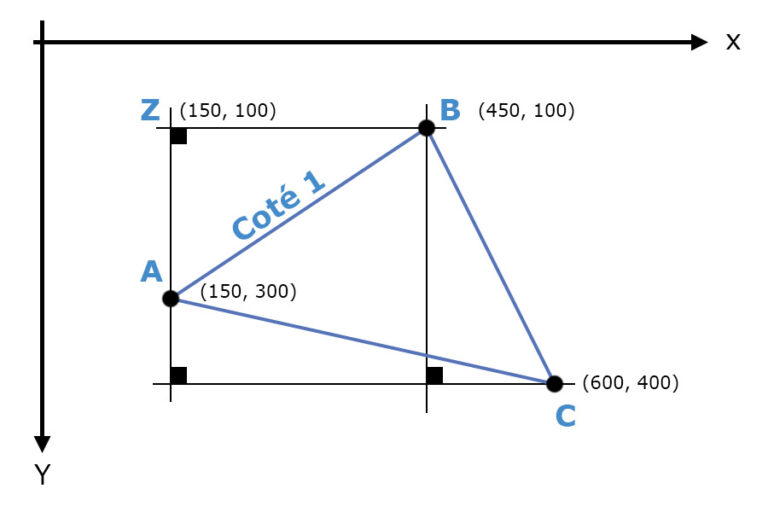
Dans cet exemple, nous créons un point Z en nous basant sur les coordonnées de A et de B.
En créant ainsi un triangle rectangle nous pouvons en calculer l’hypoténuse (coté 1) en déduisant les longueurs ZA et ZB et en appliquant le théorème de Pythagore.
3.3 – La mise en forme Informatique
Au niveau pratique nous pouvons utiliser HTML, Javascript et PHP pour réaliser une interface destinée à la saisie de points.
Dans un contexte de recherche médicale en relation avec un traitement des données par l’Intelligence Artificielle, j’avais été amené à créer une série de modules destinés à effectuer des mesures sur des séries de radiographies, à effectuer un classement en fonction des résultats et à copier les images des radiographies dans des dossiers spécifiques selon le classement.
Je vous invite à visionner la courte présentation suivante qui présente un de ces modules.
4 – Exemple complet en vidéo
Sur ma chaine Youtube Lionel Gibaudan j’ai créé une playlist qui décrit tout le processus dans une maquette HTML + Javascript+ PHP en reprenant le raisonnement exposé dans cet article
Je vous invite à consulter cette série de 8 vidéos si vous voulez mieux comprendre tous les détails du procédé.